MATLAB 图形

本章将继续探索MATLAB的绘图和图形功能。我们将讨论-

• 绘制条形图

• 绘制等高线

• 三维图

绘制条形图

bar 命令绘制二维条形图。让我们举一个实例来说明这个想法。

实例

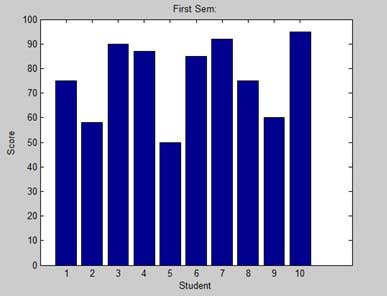
让我们有一个假想的教室，有10个学生。我们知道这些学生获得的分数百分比是75、58、90、87、50、85、92、75、60和95。我们将绘制此数据的条形图。

创建一个脚本文件并输入以下代码-

x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps

运行文件时，MATLAB显示以下条形图-

绘制等高线

两个变量的函数的等高线是一条曲线，沿该曲线函数有一个常数。等高线用于创建等高线图，方法是将给定高程（如平均海平面）上的等高点连接起来。

MATLAB提供了用于绘制等高线的函数 contour 。

实例

让我们生成一个等高线图，显示给定函数g=f(x,y)的等高线。这个函数有两个变量。因此，我们必须生成两个独立变量，即两个数据集x和y。这是通过调用meshgrid命令来完成的。

meshgrid命令用于生成元素矩阵，这些元素矩阵给出x和y的范围以及每种情况下的增量说明。

让我们绘制函数g = f(x, y)，其中−5≤x≤5，−3≤y≤3。让我们对两个值取0.1的增量。变量设置为-

[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);

最后，我们需要给函数赋值能。令我们的函数为：x ² + y ²

创建一个脚本文件并输入以下代码-

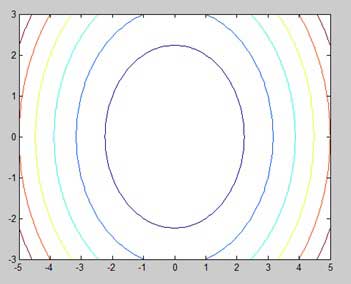
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %自变量
g = x.^2 + y.^2;                       %我们的函数
contour(x,y,g)                         %调用等高线函数
print -deps graph.eps

运行文件时，MATLAB显示以下轮廓图-

让我们稍微修改一下代码以整理映射

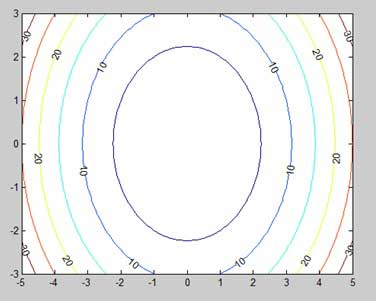
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
[C, h] = contour(x,y,g);               % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps

运行文件时，MATLAB显示以下轮廓图-

三维图

三维图基本上显示了由函数定义的两个变量g = f(x,y)的曲面。

如前所述，要定义g，我们首先使用meshgrid命令在函数的范围内创建一组(x,y)点。接下来，我们分配函数本身。最后，我们使用surf命令创建表面图。

以下示例演示了概念-

实例

让我们为函数g = xe- ^{（x 2 + y 2）}创建3D表面图。

创建一个脚本文件并输入以下代码-

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

运行文件时，MATLAB显示以下3-D映射-

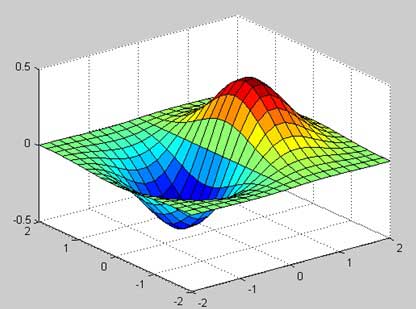
您也可以使用mesh命令生成三维表面。但是，surf命令同时以颜色显示连接线和曲面的面，而mesh命令创建的线框表面带有连接定义点的彩色线。